5.5 Experimental Extensions
JaCoP package org.jacop.floats offers also experimental extensions. They include a
method to generate constraints that define the derivative of a function, represented by
constraints, and a interval Newton method.
5.5.1 Derivatives
JaCoP can do symbolic (partial) derivatives of functions, that is using the
defined constraints for a given function and a variable defining the result of the function,
JaCoP will generate constraints that define a function for a derivative of the original function.
There is a complication in this process since constraints are not functions and sometime it is
difficult or impossible to find out which constraint defines a function for a given variable. In
such situations JaCoP uses a heuristic to find out this but it is also possible to define this
explicitly. The following examples explains the process of computing derivatives of
constrains.
Set<FloatVar> vars = new HashSet<FloatVar>(); vars.add(x1); vars.add(x2); Derivative.init(store); // Derivative.defineConstraint(x1x1, c0); // Derivative.defineConstraint(x2x2, c1); // Derivative.defineConstraint(x1x1x1x1, c2); // Derivative.defineConstraint(x2x2x2x2, c3); // ================== df/dx1 ================= FloatVar fx1 = Derivative.getDerivative(store, f, vars, x1); // ================== df/dx2 ================= FloatVar fx2 = Derivative.getDerivative(store, f, vars, x2);
In the above example, JaCoP will generate two partial derivatives 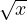 and
and 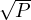 . Set vars
is used to keep all variables of function defined by variable f. The function defined by
variable f is usually defined by several constraints using temporary variables, such as x1x1,
x2x2, x1x1x1x1 and x2x2x2x2. In such situations JaCoP tries, using heuristics, to find out
what constraint defines a given temporary variable. Sometimes it is not possible and the
programmer needs to define it, as indicated by the commented code and methods
Derivative.defineConstraint. For example, constraint c0 defines variable x1x1. Method
getDerivative of class Derivative generates a variable that defines the result of the
derivative.
. Set vars
is used to keep all variables of function defined by variable f. The function defined by
variable f is usually defined by several constraints using temporary variables, such as x1x1,
x2x2, x1x1x1x1 and x2x2x2x2. In such situations JaCoP tries, using heuristics, to find out
what constraint defines a given temporary variable. Sometimes it is not possible and the
programmer needs to define it, as indicated by the commented code and methods
Derivative.defineConstraint. For example, constraint c0 defines variable x1x1. Method
getDerivative of class Derivative generates a variable that defines the result of the
derivative.
Derivatives, can be used for setting additional constraints on solutions. For example,
when looking for minimum or maximum of a function or in the interval Newton
method.
5.5.2 Multivariate Interval Newton Method
Interval Newton methods combine classical Newton method with interval analysis [9] and
are used to provide better bounds on variables.
Traditionally, univariate Newton method computes a solution for equation f(x) = 0 using
the following approximation.
This can be extended by using vector x and a Jacobian matrix instead of f′(x).
Furthermore one can extend it to interval arithmetic. This is implemented in JaCoP using
“constraint” EquationSystem. This constraint takes as parameters a vector of functions and
variables of these functions. The constraints computes then all partial derivatives and
form a set of equations that are later solved, if possible, by interval Gauss-Seidel
method.
This can be formalized as system of linear equations that, when solved, provides bounds
on values (xn+1 - xn) of variables of equations.
where F : Rk → Rk are continuously differentiable functions and JF(xn) is Jacobian
matrix.
Below, constraint eqs specifies a set of two functions f0 and f1 of two variables x1 and
x2. Constraint eqs will try to prune domains of variables x1 and x2.
EquationSystem eqs = new EquationSystem(store, new FloatVar[] {f0, f1}, new FloatVar[] {x1, x2}); store.impose(eqs);
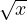 and
and 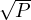 . Set vars
is used to keep all variables of function defined by variable f. The function defined by
variable f is usually defined by several constraints using temporary variables, such as x1x1,
x2x2, x1x1x1x1 and x2x2x2x2. In such situations JaCoP tries, using heuristics, to find out
what constraint defines a given temporary variable. Sometimes it is not possible and the
programmer needs to define it, as indicated by the commented code and methods
Derivative.defineConstraint. For example, constraint c0 defines variable x1x1. Method
getDerivative of class Derivative generates a variable that defines the result of the
derivative.
. Set vars
is used to keep all variables of function defined by variable f. The function defined by
variable f is usually defined by several constraints using temporary variables, such as x1x1,
x2x2, x1x1x1x1 and x2x2x2x2. In such situations JaCoP tries, using heuristics, to find out
what constraint defines a given temporary variable. Sometimes it is not possible and the
programmer needs to define it, as indicated by the commented code and methods
Derivative.defineConstraint. For example, constraint c0 defines variable x1x1. Method
getDerivative of class Derivative generates a variable that defines the result of the
derivative.

